 Sommaire
Sommaire
- Définition de l’amortissement constant
- Formules de l’amortissement linéaire
- Avantages et inconvénients dans le cadre d’un prêt immobilier
- Exemple chiffré
Définition
Le prêt à amortissement constant est un mode particulier de remboursement d’un crédit qui permet d’amortir la même part de capital à chaque échéance de remboursement et induit par conséquent une mensualité variable égale à un montant fixe de capital + une part variable d’intérêt.
À noter d’une part que l’amortissement est plus important les premières années et d’autre part que l’échéance mensuelle (capital + intérêts) est dégressive, contrairement au prêt amortissable classique pour lequel la mensualité est identique sur toute la durée tandis que le capital amorti augmente à chaque remboursement.
Formules
Quel que soit le mode d’amortissement, rappelons qu’une mensualité est constituée :
- D’une part de capital, correspondant au remboursement partiel de la dette.
- D’une part d’intérêt, correspondant au bénéfice de la banque.
Déterminer la part de capital amorti
Pour calculer l’amortissement contant, c’est-à-dire la même part de capital amorti, il suffit de diviser le capital emprunté par le nombre de mensualités de remboursement.
Am = C / n
Avec Am = Amortissement, C = capital emprunté et n = durée de l’emprunt.
Pour rappel, la formule de l’annuité constante est :
An = C * [t / – (1 – t)-n]
Avec An = annuités, C = capital emprunté, t = taux et n = durée de l’emprunt.
Déterminer la part d’intérêt
Pour trouver l’annuité de remboursement en fonction de l’annuité précédente, on applique la formule suivante :
Ip = t*[C(n-p+1)] / n
Avec I = Intérêts, p = période considérée, t = taux, C= capital emprunté et n= nombre d’années
Avantages et inconvénients dans le cadre d’un prêt immobilier
Le prêt à amortissement constant permet de rembourser une part plus importante de capital les premières années, ce a pour double effet de :
- Réduire le coût du crédit.
- Raccourcir la durée.
Un avantage intéressant pour les séniors
L’échéance mensuelle étant dégressive, les séniors peuvent anticiper sur la baisse du pouvoir d’achat qui interviendra au moment de la retraite.
Mais pas d’intérêt pour les investisseurs
L’amortissement constant est rarement utilisé par les investisseurs, contrairement au prêt in fine. Il faut avouer qu’il n’y a pas une grande différence entre les deux emprunts sur les intérêts à déduire, comme le démontre plus bas notre exemple chiffré.
Et un inconvénient dont il faut tenir compte
Les mensualités de remboursement d’un prêt immobilier à amortissement constant étant plus élevées au départ, la formule sous entend que l’emprunteur dispose de revenus plus importants que dans le cadre d’un emprunt classique.
Par ailleurs, un emprunt à échéance constante facilite la gestion du budget avec une mensualité identique jusqu’au terme, au contraire de l’amortissement linéaire.
Exemple chiffré
Considérons un prêt immobilier de 200 000 euros sur 15 ans à un taux fixe hors assurance de 1,25 %. Les résultats sont déterminés à partir d’un échéancier de remboursement mensuel. Toutefois, pour faciliter la comparaison des tableaux d’amortissement, une ligne par an seulement est reprise. Nous ne tenons pas compte de l’assurance emprunteur qui n’intervient pas dans l’amortissement du capital, mais qui doit théoriquement s’ajouter à la mensualité.
SI on emprunte sur la même durée, notez qu’il y peu d’écarts entre les deux formules au niveau des intérêts.
Exemple chiffre avec la même part de capital amorti
| Mois | Capital de début de période | Capital amorti | Intérêts | Mensualité |
| 1 | 200 000 € | 1 111,11 € | 208,3 € | 1 319,44 € |
| 12 | 187 777,78 € | 1 111,11 € | 195,33 € | 1 306,71 € |
| 24 | 174 444,44 € | 1 111,11 € | 181,71 € | 1 292,82 € |
| 36 | 161 111,11 € | 1 111,11 € | 167,82 € | 1 278,93 € |
| 48 | 147 777,78 € | 1 111,11 € | 153,94 € | 1 265,05 € |
| 60 | 134 444,44 € | 1 111,11 € | 140,05 € | 1 251,16 € |
| 72 | 121 111,11 € | 1 111,11 € | 126 16 € | 1237,27 € |
| 84 | 107 777,78 € | 1 111,11 € | 112,17 € | 1 223,38 € |
| 96 | 94 444,44 € | 1 111,11 € | 98,38 € | 1 209,49 € |
| 108 | 81 111,11 € | 1 111,11 € | 84,49 € | 1 195,6 € |
| 120 | 67 777,78 € | 1 111,11 € | 70,6 € | 1 181,71 € |
| 132 | 54 444,44 € | 1 111,11 € | 56,71 € | 1 167,82€ |
| 144 | 41 111,11 € | 1 111,11 € | 42,82 € | 1 153,93 € |
| 156 | 27 777,78 € | 1 111,11 € | 28,94 € | 1 140,05 € |
| 168 | 14 444,44 € | 1 111,11 € | 15,05 € | 1 126,16 € |
| 1 111.,1 € |
1 111,11 € |
1,16 € |
1 112,27 € |
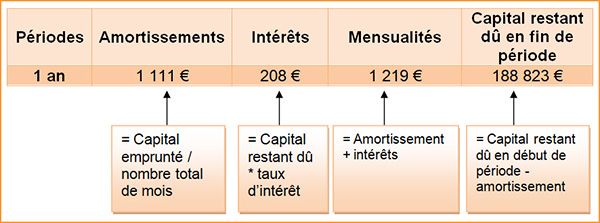
Avec la même mensualité (emprunt classique)
| Mois | Capital début de période | Mensualité | Capital amorti | Intérêts |
| 1 | 200 000,00 € | 1 219,11 € | 1 010,77 € | 208,33 € |
| 12 | 188 823,39 € | 1 219,11 € | 1 022,42 € | 196,69 € |
| 24 | 176 483,85 € | 1 219,11 € | 1 035,27 € | 183,84 € |
| 36 | 163 989,18 € | 1 219,11 € | 1 048,29 € | 170,82 € |
| 48 | 151 337,43 € | 1 219,11 € | 1 061,46 € | 157,64 € |
| 60 | 138 526,62 € | 1 219,11 € | 1 074,81 € | 144,30 € |
| 72 | 125 554,76 € | 1 219,11 € | 1 088,32 € | 130,79 € |
| 84 | 112 419,81 € | 1 219,11 € | 1 102,00 € | 117,10 € |
| 96 | 99 119,74 € | 1 219,11 € | 1 115,86 € | 103,25 € |
| 108 | 85 652,46 € | 1 219,11 € | 1 129,89 € | 89,22 € |
| 120 | 72 015,87 € | 1 219,11 € | 1 144,09 € | 75,02 € |
| 132 | 58 207,84 € | 1 219,11 € | 1 158,47 € | 60,63 € |
| 144 | 44 226,22 € | 1 219,11 € | 1 173,04 € | 46,07 € |
| 156 | 30 068,82 € | 1 219,11 € | 1 187,79 € | 31,32 € |
| 168 | 15 733,44 € | 1 219,11 € | 1 202,72 € | 16,39 € |
| 180 | 1 217,84 € | 1 219,11 € | 1 216,57 € | 1,27 € |








